Feistel ciphers

September 15, 2020

Block ciphers and Feistel networks

Block ciphers are a subfield of symmetric cryptography — that is, both parties use a single secret key to both encrypt and decrypt¹ — Rather than encode on a bit-by-bit basis, block ciphers encode entire blocks (AES, the most popular block cipher at the moment, uses 128 bit blocks)

The advantage of using blocks is that we have more degrees of freedom to substitute and shuffle around bits, so that flipping a single bit will cascade and cause changes throughout the entire block. Attackers can no longer simply flip bits and be guaranteed that it flips corresponding bits in the decrypted plaintext.

A Feistel cipher is a popular framework in which to design block ciphers. It’s widely used, most notably in the Data Encryption Standard (DES) and its extension, triple DES (3DES). That said, Feistel networks seem to include a lot of arbitrary design choices, and I’m hoping to motivate some of them here for my own peace of mind.

A graphic representation of a Feistel cipher

Here’s a basic sketch of a Feistel network.

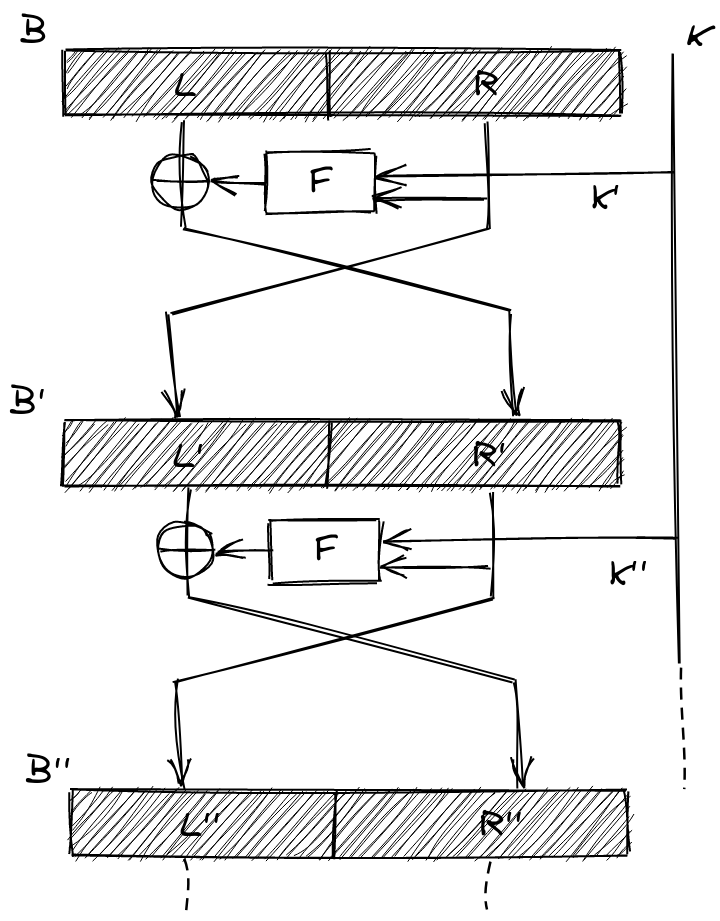
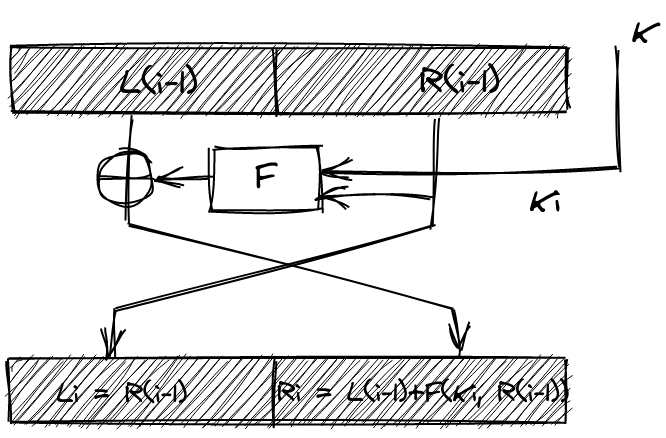
In it, we’re trying to encrypt the block $B$ using a secret key $K$. The basic operations that make up the encryption (and decryption, as we’ll see) are the XOR ($\oplus$) and the $F$ function. The procedure is essentially a single step, repeated:

We take the block $B$ and divide it up into a left block $L$ and right block $R$. We then pass $R$ through our function $F$ that will scramble the subblock, and then use it to encode $L$ by using $\oplus$. We then pass through an unencrypted copy of $R$ to the next stage! This is super-duper important! After a single round, we’ve only encrypted $L$, but because we’ve flipped the positions of $L$ and $R$ in the next stage, this time $R$ will get encrypted by running (the encrypted version of) $L$ through our scrambling function $F$. And so on…

That looks like a lot of random steps, so let’s go over some of them in more detail.

Rounds

One basic ingredient of most block ciphers is: Find an operation that only medium scrambles the bits, and then repeat that process a bunch of times to guarantee that all the bits have been thoroughly and uniformly shuffled. DES, for example, performs 16 rounds of encryption.

Why would we do this? It’s much easier to achieve a diffuse permutation of bits by repeating some process as many times as needed, than it is to find one single process that does it in one go. Probably easier to run it in reverse too.

Usually, every round will use a “round key”, a kind of “subkey” that’s derived from actual key.

Why would we do this? By mixing in a different key at every step, we’re making it so every round isn’t performing exactly the same operations over and over, making it a lot harder to trace back the encryption or infer anything from the statistics of the output.

Left/Right split

Each block gets split in two and one half is essentially used to encrypt the other. Only one half is encrypted per round!

Why would we do this? Why split the block into two? Why not simply use the key to encode the entire block, and use some other step to scramble the entire block. We’d get twice as much encrypting in if we didn’t restrict ourselves to encrypting one half at a time. One could conceive of something like the following:

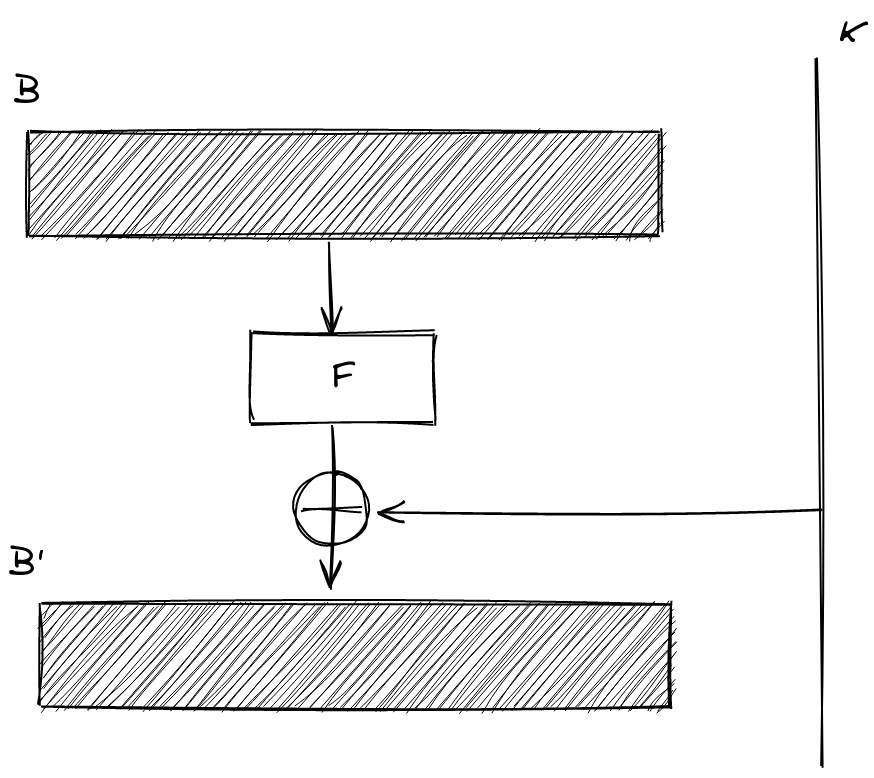
Honestly, that’s a totally viable way of doing things, and it is — in a nutshell — the way AES operates! Splitting the block into left and right has some cool benefits, though.

Decryption

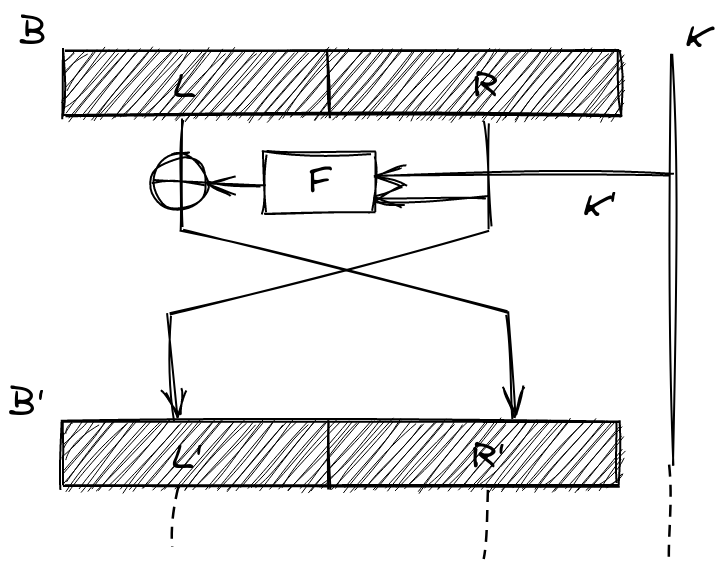
The cool thing about the $L$/$R$ split is the following. Suppose we want to start decrypting our block by running this algorithm in reverse from the end.

The block we’ve received is $(L_i, R_i)$, which we can write in terms of the previous round as $(R_{i-1},\, L_i\oplus F(K_i, R_i-1))$. What we want to get if we’re to run this whole thing in reverse, is $L_{i-1}$ and $R_{i-1}$, and then work our way back from there. Well, since every step only encrypts half a block, we’ve already got $R_{i-1}$ for free! Since $L_i$ is encrypted with an $\oplus$, the way we decrypt is by simply XOR’ing with the same bits. That is, to recover $L_{i-1}$, we need to XOR a second time with $F(K_i, R_{i-1})$. And here’s the kicker: precisely because we only encrypted half of the block, and passed through $R_i$ unchanged, we can simply recompute $F(K_i, R_{i-1})$ ourselves! ² We can then just perform the XOR to decode $L_{i-1}$ and start all over again. Notice how the decryption of a round is identical to encryption: We take one half, run it through $F$ and XOR it with the other half!

Involution

In fact, an even cooler way of thinking about decrypting is the following: you just run the whole encryption a second time! The only thing that changes between Feistel encryption and decryption is that the round keys that are used in each step are reversed, so that we start decrypting the last encryption round $n$ with its corresponding key $K_{n}$. Of course we can only decrypt round $i$ with the corresponding key $K_i$! You could say Feistel encryption is an involution: it’s its own inverse.

Why would we do this? Having encryption and decryption being the exact same operation makes implementing it a lot easier. Important block ciphers are often implemented on the hardware level: your x86 CPU literally has instructions to perform AES encryption. Feistel ciphers cut the work needed to implement this in half. This is particularly interesting when we’re talking about smaller, more constrained devices like smart cards.

One-way function

Another cool thing about this decryption method: We never have to reverse the encryption function $F$! Even when we’re decrypting, we only apply $F$, we never have to make use of some inverse operation $F^{-1}$. We could use completely irreversible functions, so called one-way function.

Why would we do this? This is huge, because it means we can go all out with how we design our encryption function $F$. We can do computationally infeasible things like big modulo exponentiations, or even throw bits away all together. The sky is the limit! In an encryption scheme like AES, where the encryption has to be run in reverse, there are much bigger constraints on what operations you can tractably decrypt.

Framework

Like we said, Feistel ciphers are only a framework. There are a bunch of parameters in this construction that you can fix. The most obvious one being the choice of encryption function $F$. But also the number of rounds, the block size, or even whether or not the blocks should be of equal size or not ( so called unbalanced Feistel ciphers). Also, we didn’t go into the key schedule at all. That is: the key size ³ or how the round keys $K_i$ are derived from the secret key $K$.

Hope this helped clear up some of the (seemingly) arbitrary aspects of Feistel networks!

Footnotes

1. This is different from public key or _asymmetrc cryptography where there is usually a public and private key, where one is used for encryption and the other for decryption. ↩

2. Given we have the secret key, $K_i$, of course! ↩

3. This is actually DES’ main flaw: it only uses a 56bit key, which was plenty strong when it was first developed in 1975, but has now been broken on several occasions. ↩